Complete list
A curated, up to date list of publication is available at my Web of Science profile .
Reviews

Benchmark Calculations of Interaction Energies in Noncovalent Complexes and Their Applications
Řezáč, J.; Hobza, P. Chem. Rev. 2016, 116 (9), 5038–5071.
A review summarizing my and related work on accurate calculations of non-covalent interactions and data sets of benchmark data. It is a part of a thematic issue on non-covalent interactions for which I, together with Pavel Hobza, served as a guest editor.
Important publications

Non-Covalent Interactions Atlas benchmark data sets
Five papers introducing the NCIAtlas data sets:
Řezáč, J. Phys. Chem. Chem. Phys. 2022, 24 (24), 14780–14793.
Kříž, K.; Řezáč, J. Phys. Chem. Chem. Phys. 2022, 24 (24), 14794–14804.
Kříž, K.; Nováček, M.; Řezáč, J. J. Chem. Theory Comput. 2021, 17 (3), 1548–1561.
Řezáč, J. J. Chem. Theory Comput. 2020, 16 (10), 6305–6316.
Řezáč, J. J. Chem. Theory Comput. 2020, 16 (4), 2355–2368.

Description of halogen bonding in semiempirical quantum‐mechanical and self‐consistent charge density‐functional tight‐binding methods
Řezáč, J. J. Comput. Chem. 2019, 40 (17), 1633-1642.
Detailed analysis of how semiempirical QM methods PM6 and PM7, and DFTB3, describe halogen bonding. The classical SQM methods are able to describe the sigma-hole, and the errors can be attributed to other tems. On the other hand, DFTB3, with its monopole approximation, fails to describe the electrostatic component properly.
Toward Accurate Conformational Energies of Smaller Peptides and Medium-Sized Macrocycles: MPCONF196 Benchmark Energy Data Set
Řezáč, J.; Bím, D.; Gutten, O.; Rulíšek, L. J. Chem. Theory Comput. 2018, 14 (3), 1254-1266.
Benchmark data set of conformation energies of peptides and macrocycles. The peptide part is a more accurate recalculation of our prior work including the PCONF set.

Empirical Self-Consistent Correction for the Description of Hydrogen Bonds in DFTB3
Řezáč, J. J. Chem. Theory Comput. 2017, 13 (10), 4804-4817.
Novel correction for hydrogen bonding in DFTB methods. Modifying the description of the electrostatic interactions in the DFTB Hamiltonian, it achieves accuracy superior to the previous standalone correction despite using less parameters.
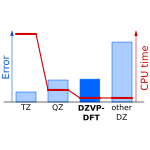
Accurate DFT-D3 Calculations in a Small Basis Set
Hostaš,J.; Řezáč, J. J. Chem. Theory Comput. 2017, 13, 3575–3585.
We have found that among may double-zeta sized basis set, the DZVP-DFT yields very small basis set superposition error. When combined with reparameterized D3 dispersion correction, DFT calculations in this basis are as accurate as DFT-D3 calculations in triple-zeta basis set but the computational cost is much lower.
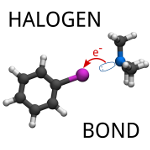
On the role of charge transfer in halogen bonding
Řezáč, J.; de la Lande, A. Phys. Chem. Chem. Phys. 2017, 19, 791-803.
We have separated the contribution of charge transfer to the interaction energy of halogen bonds. We found that this contribution is rather small, up to 10% of the interaction energy, what is slightly less than in hydrogen bonds. It becomes larger in extremely strong halogen bonds but even there, it is similarly small when compared to the other attractive contributions.
Benchmark Calculations of Three-Body Intermolecular Interactions and the Performance of Low-Cost Electronic Structure Methods
Řezáč, J.; Huang, Y.; Hobza, P.; Beran, G. J. O. J. Chem. Theory Comput. 2015, 11 (7), 3065–3079.
Extension of our benchmarking to three-body interaction energies. 69 model systems taken from 23 crystals map three-body interactions with varying proportion of polarization and London dispersion. The study revealed severe issues in the description of the theree-body polarization by many DFT functionals.
Robust, Basis-Set Independent Method for the Evaluation of Charge-Transfer Energy in Noncovalent Complexes
Řezáč, J.; de la Lande, A. J. Chem. Theory Comput. 2015, 11 (2), 528–537.
A novel method of defining and quantifying intermolecular charge transfer. It uses a spatial definition of the molecular fragments what makes it independent on basis set size (unlike orbital-based definitions). Constrained DFT is then used to separate the contribution of charge transfer to the interaction energy.
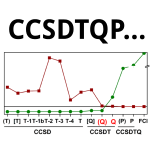
Convergence of the Interaction Energies in Noncovalent Complexes in the Coupled-Cluster Methods Up to Full Configuration Interaction
Šimová, L.; Řezáč, J.; Hobza, P. J. Chem. Theory Comput. 2013, 9 (8), 3420–3428.
One part of our project mapping the accuracy of post-CCSD(T) methods applied to non-covalent interactions. The major conclusion is that CCSDT(Q) is the most economical approach that corrects majority of effects missing in CCSD(T). The accuracy is then limited mostly by basis set size.
Benchmark calculations of noncovalent interactions of halogenated molecules (X40 data set)
Řezáč, J.; Riley, K. E.; Hobza, P. J. Chem. Theory Comput. 2012, 8 (11), 4285–4292.
Benchmark data set covering interaction sof halogenated organic molecules, with special focus on halogen bonding.

Advanced Corrections of Hydrogen Bonding and Dispersion for Semiempirical Quantum Mechanical Methods
Řezáč, J.; Hobza, P. J. Chem. Theory Comput. 2012, 8 (1), 141–151.
The last and best from our series of corrections for hydrogen bonding and dispersion in semiempirical QM methods. The corrected PM6-D3H4 method became the basis of a large computer-aided drug design project running in our group.

S66: A Well-balanced Database of Benchmark Interaction Energies Relevant to Biomolecular Structures
Řezáč, J.; Riley, K. E.; Hobza, P. J. Chem. Theory Comput. 2011, 7 (8), 2427–2438.
The core data set covering non-covalent interactions in organic molecules, intended for method testing and parametrization. It has been extended with dissoaciation curves (S66x8) and angular displacements (S66a8) for all the systems.